Modeling
Deep foundation pile model
- when: 03/2019 - 06/2019
- organization: Chalmers University of Technology
- course: Deep Foundations
This task was performed as part of the design project in the course on deep foundations I took during my masters degree at Chalmers University of Technology. The task was to design the deep piles below a tunnel structure located in Gothenburg, Sweden. The piles were to be designed as tension piles due to the soft clay type soil in Gothenburg.
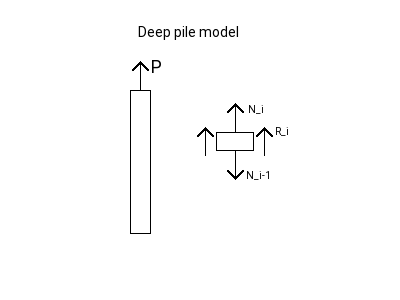
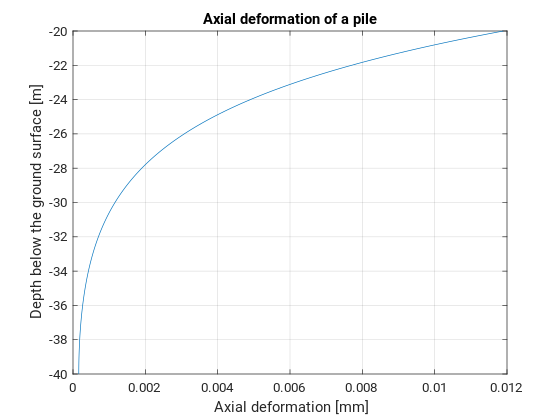
To perform the analysis required to design the deep piles, I wrote a MATLAB script to compute the deformations and forces which would be experienced by the axially-loaded piles. The piles were discretised into n elements with axial load and soil resistance as shown below.
Non-linear finite element material modeling
- when: 01/2019 - 03/2019
- organization: Chalmers University of Technology
- course: Finite element method (Structures)
This task was accomplished as part of a advanced finite element (FE) course I took at Chalmers University of Technology to illustrate my ability to perform non-linear FE modeling. The analysis consisted of determining the deformation and stress field of a steel pipe with a longitudinal weld by writing a MATLAB script implementing the solution using non-linear methods. The idea here is to determine the maximum force required to open a gap where the weld would exist in order to identify the weld strength required. The problem geometry is shown below.
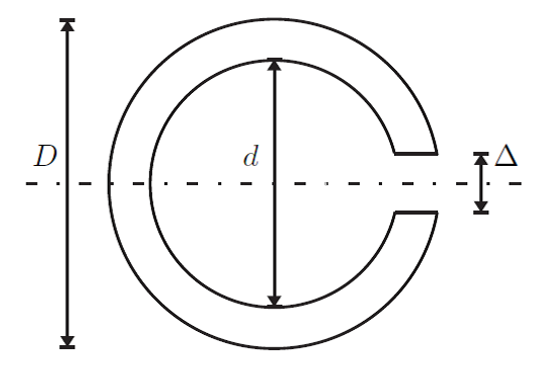
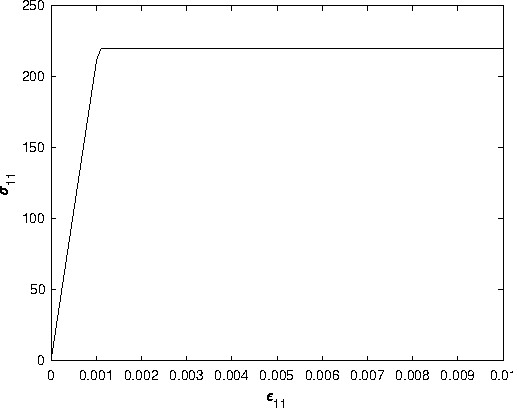
In this problem, the so-called Hencky plasticity material model is used to capture the non-linear behaviour which can be identified by a uniaxial strain check of the FE model shown below. Both the deformed shape and stress distribution can than be computed using the FE model.
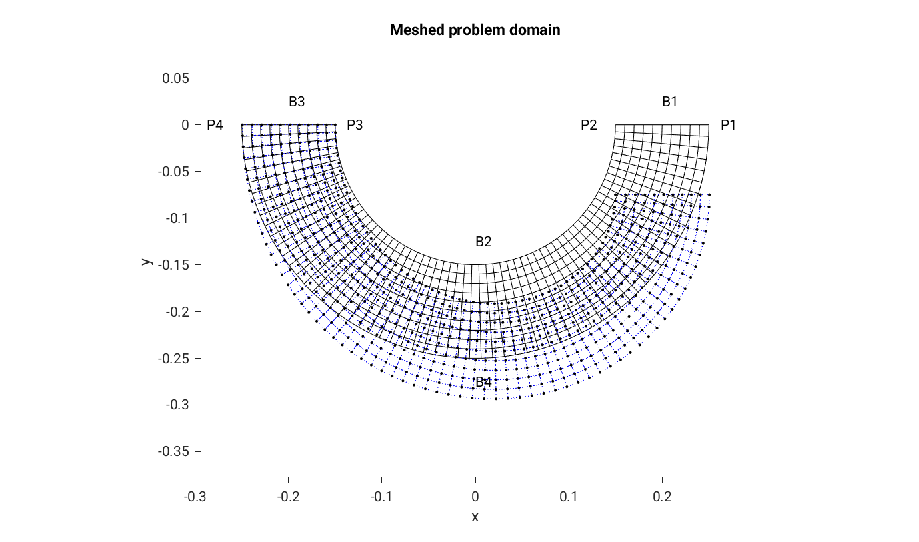
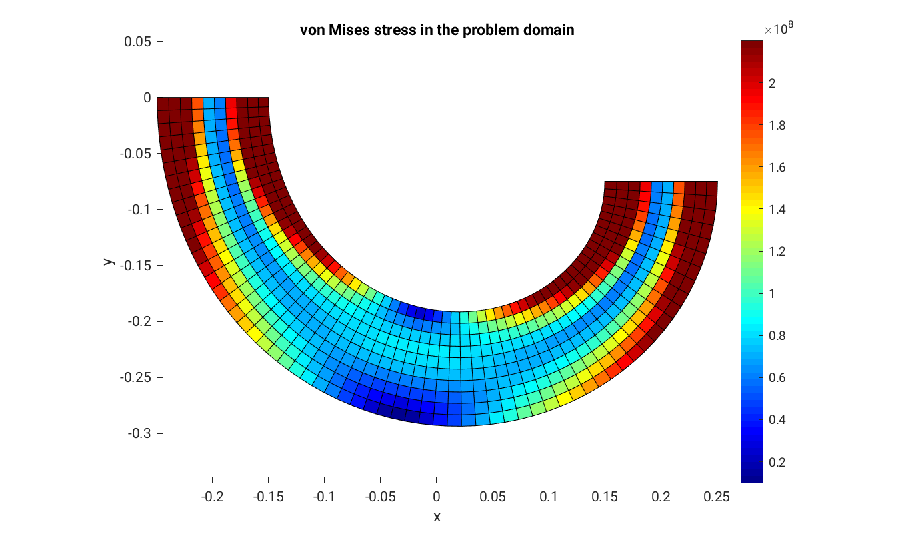
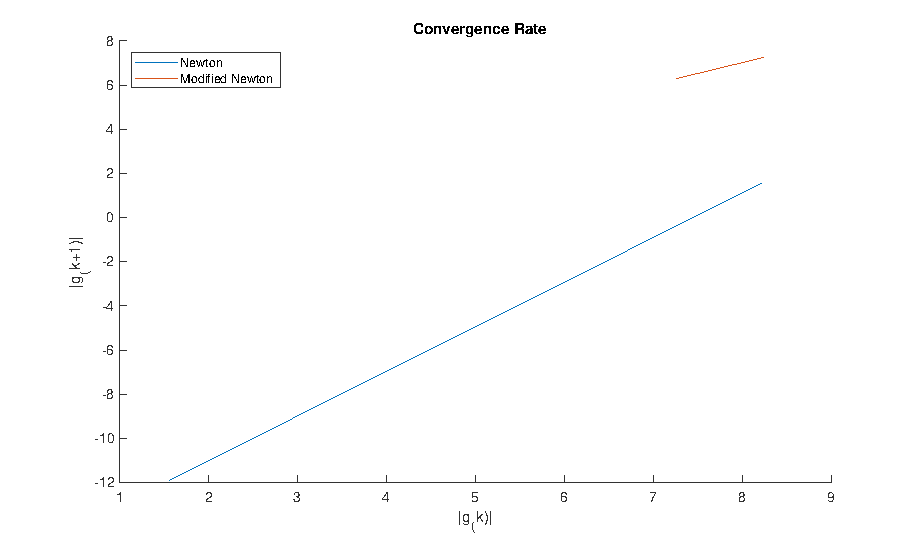
Additionally, the non-linear FE method requires a iterative approach to arrive at the solution whereby both the Newton and modified Newton algorithms were used and compared in terms of convergence rates (see below). Verification and validation of the MATLAB script was performed with the commercial FE software ABAQUS.
All code and documentation can be found on my GitLab repository for this project.